什么是37％法则？

这玩意经常被冠以「教你找到最优人生伴侣」的噱头，但其实没什么意义。
设想这样一个问题，你需要在麦田中选摘一支最大的麦穗，要求是不能走回头路且只能摘一支，采取何种策略成功概率最大？
显然过早摘取会错过后面还没见过的麦穗、过晚摘取则会对早期遇到的大麦穗追悔莫及。
一种直观的思路是，首先走过前100个的麦穗，这期间仅仅观察大小而不摘取。
然后继续走过其余的麦穗，一旦遇到某个比最初100个都大的麦穗，就摘取作为结果。
当然，此处的100是随口举的例子。假设麦穗的总数为 $n$ ，那么我们需要选取一个最合适的位置 $m$ ，对于遇到的前 $m$ 个麦穗仅观察不摘取，从第 $m+1$ 个麦穗开始，一旦遇到比此前都大的，就摘取它。
注意到在 $n$ 个麦穗中，每个麦穗是全局最大麦穗的概率都是 $\frac{1}{n}$ .
如果最大的麦穗在前 $m$ 个中，那么由于仅仅观察而没有摘取，这种情形下一定会失败。
如果最大的麦穗恰好是第 $m+1$ 个麦穗，那我们观察完毕后立即就遇到了比前面都大的麦穗，于是成功找到了最大的，这种情形下一定成功。
如果最大的麦穗恰好是第 $m+2$ 个麦穗，那我们观察完毕后，再过一个就会遇到最大的麦穗，看上去很容易成功？但是要谨防在此之前，如果遇到的第 $m+1$ 个麦穗已经满足比前面都大（即使它不是全局最大的），那么就会错误地摘取第 $m+1$ 个麦穗作为结果。注意到这 $m+1$ 个麦穗中第 $m+1$ 个麦穗比前面的麦穗都大的概率为 $\frac{1}{m+1}$ ，也就是说有 $\frac{1}{m+1}$ 的概率策略会非常不幸地失败，即成功概率为 $\frac{m}{m+1}$ .
如果最大的麦穗恰好是第 $m+3$ 个麦穗，观察完毕后，再过两个就会遇到真正最大的麦穗。要谨防这两个麦穗其中之一是前 $m+2$ 个麦穗中最大的，这种不幸的情况发生概率为 $\frac{2}{m+2}$ ，即成功概率为 $\frac{m}{m+2}$.
同理，如果如果最大的麦穗恰好是第 $n$ 个麦穗（也就是最后一个麦穗），成功的概率就是 $\frac{m}{n-1}$ .
那么综合所有情形，此种策略的成功概率为

$P(n,m)=\displaystyle\frac{1}{n}\displaystyle\sum_{k=m}^{n-1} \frac{m}{k}$

当 $n$ 足够大时，有

$P(n,m)=\displaystyle\frac{m}{n}\sum_{k=m}^{n-1}\frac{1}{k}=\displaystyle\frac{m}{n}\int_{m}^{n}\frac{1}{x}\mathrm{d}x=\frac{m}{n}\ln\frac{n}{m}$

众所周知， $f(x)=x\ln\frac{1}{x}$ 在 $[0,1]$ 的图像为

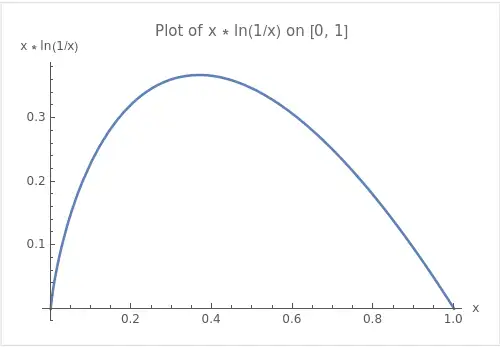
由于 $f'(x)=-\ln x-1$ ，故 $f$ 在 $\frac{1}{e}$ 处取得最大值，甚至最大值也是 $\frac{1}{e}$ .
也就是说，观察数量 $m$ 和总数量 $n$ 的最佳比例是 $\frac{1}{e}=37\%$ ，此时有 $37\%$ 的概率能找到最大的麦穗（真是 Amazing 啊， $e$ 又以一种意想不到的方式出现了）。
所以我为什么说没多大意义呢？这个策略需要你已知麦穗的总数，并且还需要麦穗足够多，才只有 $37\%$ 的概率取得最优结果（即使这是最好的策略）。而在寻找人生伴侣这件事情上，你并不知道总共会有多少个可让你观察的对象，也没有足够多的对象数量供你尝试。
所以，还真是遗憾啊 XD