LN1

Alphabets and Strings

An alphabet is a set of symbols
String: a sequence of symbols from some alphabet
Language: a set of strings
Unary numbers alphabet $\Sigma=\{1\}$
Unary number: 1 11 111...

String Operations

• Concatenation $wv$
• Reverse $w^R$
• String Length $|w|$
  Empty String: A string with no letters is denoted: $\varepsilon$ or $\lambda$
• Substring: a subsequence of consecutive characters
• Prefix and Suffix $w=uv$ $u$ is prefix and $v$ is suffix
• Exponent Operation: $w^n=\underbrace{ww\cdots w}_{n}$ and $w^0=\varepsilon$
• The * Operation
  $\Sigma^*$ :the set of all possible strings from alphabet $\Sigma$
• The + Operation
  $\Sigma^+=\Sigma^*-\{\varepsilon\}$

Languages

A language over alphabet $\Sigma$ is any subset of $\Sigma^*$

Empty language $\{\}$ or $\varnothing$

Operations on Languages

• The usual set operations: union, intersection, difference, complement
• Reverse: $L^R=\{w^R: w\in L\}$
• Concatenation: $L_1L_2=\{ xy:x\in L_1,y\in L_2 \}$
  $L^0=\{\varepsilon\}$
• Star-Closure (Kleene *)
  All strings that can be constructed from $L$
  $L^*=L^0\cup L^1\cup L^2\cup\cdots$
• Positive Closure
  $L^+=L^1\cup L^2\cup\cdots$

LN2 Deterministic Finite Automata

For every state, there is a transition for every symbol in the alphabet

Formal Definition
Deterministic Finite Automaton (DFA)
$M=(Q,\Sigma,\delta,q_0,F)$

• $Q$: set of states
• $\Sigma$: input alphabet $\varepsilon\notin\Sigma$ (:the input alphabet never contains empty string)
• $\delta$: transition function
  $\delta:Q\times\Sigma\rightarrow Q, \delta(q_0,a)=q_1$
  Extended Transition Function $\delta^*(q,w)=q'$
  Describes the resulting state after scanning string $w$ from state $q$
• $q_0$: initial state
• $F$: set of accepting states

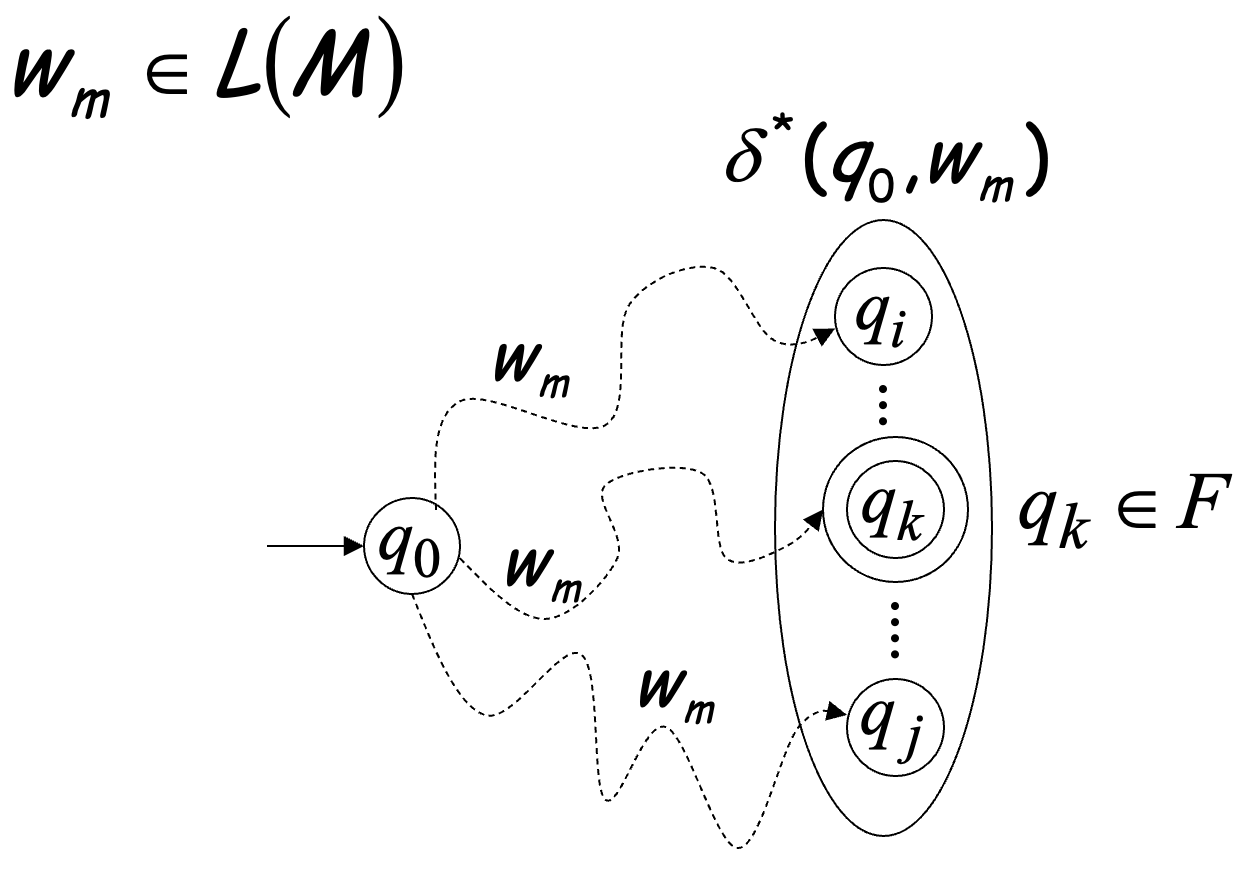
Language Accepted by DFA
Language accepted by $M$
$L(M)=\{w\in\Sigma^*:\delta^*(q_0,w)\in F\}$
Language rejected by $M$

Regular Languages
A language $L$ is regular if there is a DFA $M$ that accepts it, which means $L(M)=L$
The languages accepted by all DFAs form the family of regular languages

LN3 Non-Deterministic Finite Automata

A NFA accepts a string:
if there is a computation path of the NFA that accepts the string.
all the symbols of input string are processed and the last is an accepting state2

A NFA rejects a string:
if there is no computation of the NFA that accepts the string.
For each possible computation path:
All the input is consumed and the automaton is in a non accepting state
or
The input cannot be consumed

• $\delta$: transition function
  $\delta(q_0,x)=\{q_1,q_2,\cdots,q_k\}$ (can be $\varnothing$)

Note that for any state $q, q\in \delta^*(q, \varepsilon)$

Equivalence of Machines
Machine $M_1$ is equivalent to machine $M_2$ if $L(M_1)=L(M_2)$
Languages accepted by NFAs = Regular Languages (aka Languages accepted by DFAs)

NFAs and DFAs have the same computation power, namely, they accept the same set of languages.

Proof:

1. Languages accepted by NFAs $\supseteqq$ Regular Languages. Because every DFA is trivially a NFA;
2. Languages accepted by NFAs $\subseteqq$ Regular Languages. Becasue any NFA can be converted to an equivalent DFA(We will show it later).

Conversion Procedure Steps

1. Initial state of NFA is $q_0$ and $\delta^*(q_0, \varepsilon)=\{q_0,\cdots\}$, so that initial state of DFA is $\{q_0,\cdots\}$;
2. For every DFA’s state $\{q_i,\cdots, q_j\}$, compute in the NFA $\delta^*(q_i,a)\cup\cdots\cup\delta^*(q_j,a)\rightarrow \{q_l',\cdots,q_n'\}$, then add transition to DFA $\delta(\{q_i,\cdots, q_j\}, q)=\{q_l',\cdots,q_n'\}$;
3. Repeat Step 2 for every state in DFA and symbols in alphabet until no more states can be added in the DFA;
4. For any DFA state $\{q_i,\cdots, q_j\}$, if some $q_j$ is accepting state in NFA, then $\{q_i,\cdots , q_j\}$ is accepting state in DFA.

LN4 Properties of Regular Languages

We say Regular languages are closed under

• Union $L_1\cup L_2$
• Concatenation $L_1L_2$
• Star $L_1^*$
• Reversal $L_1^R$
• Complement $\overline{L_1}$
• Intersection $L_1\cap L_2$

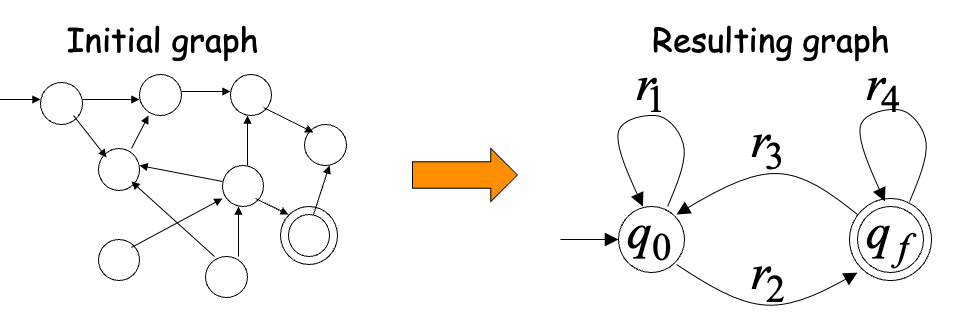
Every NFA(also include NFA without accepting state) is equivalent to a NFA which contains single accept state.

LN5 Regular Expressions

Regular Expressions

Regular expressions describe regular languages
$(a+b\cdot c)^*$ describes the language $\{a,bc\}^*=\{\varepsilon,a,bc,aa,abc,bca,bcbc,\cdots \}$

Primitive regular expressions: $\varnothing, \varepsilon, a$
Given regular expressions $r_1,r_2$, $r_1+r_2,r_1\cdot r_2, r_1^*, (r_1)$ are regular expressions

Languages of Regular Expressions

$L(r)$ means langguage of regular expression $r$
$L(\varnothing)=\varnothing$
$L(\varepsilon)=\{\varepsilon\}$
$L(a)=\{a\}$
$L(r_1+r_2)=L(r_1)\cup L(r_2)$
$L(r_1\cdot r_2)=L(r_1)L(r_2)$
$L(r_1^*)=(L(r_1))^*$
$L((r_1))=L(r_1)$

Equivalent Regular Expressions

Theorem:Languages Generated by Regular Expressions = Regular Languages

$r=r_1^*r_2(r_4+r_3r_1^*r_2)^*$

When we say we are given a Regular Language $L$, we mean Language $L$ is in a standard representation (DFA, NFA, or Regular Expression)

LN6 Regular Grammars

Gramars

Grammar $G=(V,T,S,P)$

$S\rightarrow aSb$
$S\rightarrow\lambda$

• $V$: Set of variables $V=\{S\}$
• $T$: Set of terminal symbols $T=\{a,b\}$
• $S$: Start variable
• $P$: Set of Production rules $P=\{S\rightarrow aSb, S\rightarrow\lambda\}$

Sentential Form :A sentence that contains variables and terminals

Language of a Grammar

For a grammar $G$ with start variable $S$
$L(G)=\{w:S\xRightarrow{*} w\}$ $w$ is one string of terminals
$A\rightarrow aAb|\lambda$

Linear Grammars

Linear Grammars: Grammars with at most one variable at the right side of a production

A Non-Linear Grammar
$S\rightarrow SS | \lambda | aSb | bSa$
$L(G) = \{w:n_a(w)=n_b(w)\}$ $n_a(w)$ means number of $a$ in string $w$

Right-Linear Grammars:
All productions have form $A\rightarrow xB$ or $A\rightarrow x$

Left-Linear Grammars:
All productions have form $A\rightarrow Bx$ or $A\rightarrow x$

Regular Grammars

A regular grammar is any right-linear or left-linear grammar
Regular grammars generate regular languages
Theorem Languages Generated by Regular Grammars Regular Languages = Regular Languages
For any transition $q\xrightarrow{a}p$ add production $a\rightarrow ap$
For any final state $q_f$ add production $q_f\rightarrow \lambda$

LN7-8 Non-regular languages (Pumping Lemma)

Non-regular languages

$\{ a^nb^n:n\ge 0\}$
$\{vv^R:v\in\{a,b\}^*\}$

The Pigeonhole Principle and DFAs

Considering number of states of DFA is $p$, for a walk of $w$, if $|w|\ge p$, which means numbers of states in walk is at least $p+1$, then a state is repeated in the walk $w$

The Pumping Lemma

Take an infinite regular language, $L$ There exists a DFA that accepts $L$
Take string $w\in L$ with $|w|\ge p$, then, at least one state is repeated in the walk of $w$
Take $q$ to be the first state repeated
We can write $w=xyz$, Where $y$ corresponds to substring between first and second occurrence of $q$
Note that $|xy|\le p$, because of unique states in $xy$ (Since, in $xy$ no state is repeated execpt $q$)
Since there is at least one transition in loop, $|y|\ge 1$
We do not care about the form of string $z$ ($z$ may actually overlap with the paths of $x$ and $y$)
In General, the string $xy^iz$ is accepted $i=0,1,2$
Therefore, $xy^iz\in L,i=0,1,2,\cdots$

The Pumping Lemma:

• Given a infinite regular language $L$
• there exists an integer $p$ (critical length)
• for any string $w\in L$ with length $|w|\ge p$
• we can write $w=xyz$
• with $|xy|\le p$ and $|y|\ge 1$
• such that $xy^iz\in L,i=0,1,2,\cdots$

Applications of the Pumping Lemma

Every language of finite size has to be regular
Therefore, every non-regular language has to be of infinite size

$L=\{ a^nb^n:n\ge 0\}$
Assume for contradiction that $L$ is a regular language
Since $L$ is infinite we can apply the Pumping Lemma
Let $p$ be the critical length for $L$
We pick $w=a^pb^p$
We can write $y=a^k,1\le k\le p$
Thus $xy^2z\in L,a^{p+k}b^p\in L$
But $a^{p+k}b^p\notin L$, CONTRADICTION!!!

LN9 Context-Free Languages

Context-Free Grammars

Grammar $G=(V,T,S,P)$

$G: S\rightarrow aSb | SS | \varepsilon$
$L(G)$ Describes matched parentheses: $((())())(())$

Derivation Order and Derivation Trees

$S\rightarrow AB, A\rightarrow aaA | \varepsilon, B\rightarrow Bb | \varepsilon$

derivation	1	2	3	4	5	6
leftmost	$S$	$AB$	$aaAB$	$aaB$	$aaBb$	$aab$
rightmost	$S$	$AB$	$ABb$	$Ab$	$aaAb$	$aab$

They give same derivation tree

Ambiguity

A context-free grammar $G$ is ambiguous if there is a string $w\in L(G)$ which has:
two different derivation trees or two leftmost derivations (Two different derivation trees give two different leftmost derivations and vice-versa)

In general, ambiguity is bad and we want to remove it
Sometimes it is possible to find a non-ambiguous grammar for a language
But, in general ιt is difficult to achieve this

LN10 Simplifications of Context-Free Grammars

A Substitution Rule

Nullable Variables $\varepsilon$-production
Unit-Productions
Useless Productions

Normal Forms for Context-free Grammars

Chomsky Normal Form Each production has form: $A\rightarrow BC$ or $A\rightarrow a$
Conversion to Chomsky Normal Form
It is easy to find the Chomsky normal form for any context-free grammar (which doesn’t generate $\varepsilon$)

Greinbach Normal Form All productions have form: $A\rightarrow aV_1V_2\cdots V_k, k\ge 0$
Greinbach normal forms are very good for parsing strings (better than Chomsky Normal Forms)
However, it is difficult to find the Greinbach normal of a grammar

LN11 Properties of Context-Free languages

Closed

• Union $S\rightarrow S_1 | S_2$
• Concatenation $S\rightarrow S_1S_2$
• Star Operation $S\rightarrow S_1S | \lambda$

Negative Properties of Context-Free Languages (not closed)

• Intersection
• Complement

$L_1=\{a^nb^nc^m\},L_2=\{a^nb^mc^m\}$

Intersection of Context-free languages and Regular Languages(Applications of Regular Closure)

The intersection of a context-free language and a regular language is a context-free language
Prove that $L=\{w:n_a=n_b=n_c\}$ is not context-free
Becasue $L_2=\{a^*b^*c^*\}$ is regular, $L\cap L_2=\{a^nb^nc^n\}$ is not context-free.
So it's impossible that $L$ is context-free

LN12 Pushdown Automata PDAs

Pushdown Automaton -- PDA

Initial Stack Symbol

The States

• replace: $a,b\rightarrow c$
• push: $a,\varepsilon\rightarrow c$
• pop: $a,b\rightarrow\varepsilon$
• no change: $a,\varepsilon\rightarrow\varepsilon$

PDAs are non-deterministic
Allowed non-deterministic transitions

A string is accepted if there is a computation such that:
All the input is consumed AND The last state is an accepting state
we do not care about the stack contents at the end of the accepting computation

Formalities for PDAs

Pushdown Automaton (PDA)
$M = (Q, \Sigma, \Gamma, \delta, q_0, z, F)$

• $Q$ state
• $\Sigma$ Input alphabet
• $\Gamma$ Stack alphabet
• $\delta$ Transition function $\delta(q_1,a,w_1)=\{(q_2,w_2),(q_3,w_3)\}$
• $q_0$ Initial state
• $z$ Stack start symbol
• $F$ Accept states
  $(q,u,s)$
• $q$ Current state
• $u$ Remaining input
• $s$ Current stack content

$(q_1, bbb, aaa\$) \succ (q_2, bb, aa\$)$

Language $L(M)$ accepted by PDA $M$:

$L(M)=\{w:(q_0,w,z)\overset{*}{\succ} (q_f,\varepsilon,s)\}$

LN13 PDAs Accept Context-Free Languages

Theorem: Context-Free Languages (Grammars) = Languages Accepted by PDAs

Convert Context-Free Grammars to PDAs

For each terminal $a$ in $G$, add $a,a\rightarrow\varepsilon$
For each production $A\rightarrow w$ in $G$, add $\varepsilon, A\rightarrow w$
e.g. $G: S\rightarrow aSTb|b, T\rightarrow Ta|\varepsilon$
PDA: $\varepsilon,S\rightarrow aSTb;\varepsilon,S\rightarrow b;\varepsilon,T\rightarrow Ta; \varepsilon,T\rightarrow \varepsilon;a,a\rightarrow \varepsilon;b, b\rightarrow \varepsilon$

Grammar Leftmost Derivation
$\begin{array}{l} S\\ \Rightarrow aSTb \\ \Rightarrow abTb \\ \Rightarrow abTab \\ \Rightarrow abab\end{array}$

PDA Computation

$\begin{array}{l} (q_0, abab, \$) \\ \succ (q_1, abab, S\$) \\ \succ (q_1, bab, STb\$) \\ \succ (q_1, bab, bTb\$) \\ \succ (q_1, ab, Tb\$) \\ \succ (q_1, ab, Tab\$) \\ \succ (q_1, ab, ab\$) \\ \succ (q_1, b, b\$) \\ \succ (q_1, \varepsilon, \$) \\ \succ(q_2, \varepsilon, \$) \\ \end{array}$

Grammar $G$ generates string $w$ $S\xRightarrow{*}w$ if and only if PDA $M$ accepts $w$ $(q_0,w,\$)\overset{*}{\succ} (q_2,\varepsilon,\$)$

Convert PDAs to Context-Free Grammars

Too long to wirte down here

LN14 DPDA Deterministic PDA

Definition

$L(M)=\{a^nb^n:n\ge 0\}$ is DPDA
$L(M)=\{vv^R:v\in\{a,b\}^*\}$ is not DPDA
because $?,a\rightarrow b;?,a\rightarrow c$ is not allowed in DPDA

PDAs Have More Power than DPDAs

We will show that there exists a context-free language $L$ which is not accepted by any DPDA
Which means Deterministic Context-Free Languages(DPDA) $\subsetneqq$ Context-Free
Languages(PDA)

e.g. $L=\{a^nb^n\}\cup \{a^nb^{2n}\}$ is context-free but not deterministic context-free
Because if there is a DPDA accept $L$, we will get a DPDA accepting $\{a^nb^nc^n\}$ by modifying $M$, replacing $b$ with $c$
The language $\{a^nb^nc^n\}$ is not context-free(we can prove this using pumping lemma later)

LN15-16 Pumping Lemma for Context-free Languages

The Pumping Lemma:
For any infinite context-free language $L$
there exists an integer $p$ such that
for any string $w\in L,|w|\ge p$
we can write $w=uvxyz$
with length $|vxy|\le p$ and $|vy|>0$
and it must be that: $uv^ixy^iz\in L,\forall i\in \mathbb{N}$

LN17 Turing Machines

Turing Machines are deterministic
The tap with infinite length
The head at each transition (time step):

1. Reads a symbol
2. Writes a symbol
3. Moves Left or Right
   Turing Machines are deterministic(No $\varepsilon$-transitions allowed)
   No transition for input symbol is allowed

Halting

The machine halts in a state if there is no transition to follow
Accepting states have no outgoing transitions
The machine halts and accepts
Accept Input String = If machine halts in an accept state
Reject Input String = If machine halts in a non-accept state or If machine enters an infinite loop
In order to accept an input string, it is not necessary to scan all the symbols of the input string

Formal Definitions for Turing Machines

$M=(Q,\Sigma,\Gamma,\delta,q_0,\lozenge,F)$
$\lozenge$: Blank
A move $q_0 xayb\succ x q_1 ayb$
$L(M)=\{w:q_0w\overset{*}{\succ} x_1q_fx_2\}$
If a language $L$ is accepted by a Turing machine then we say that is:

• Turing Recognizable
• Turing Acceptable
• Recursively Enumerable

LN18 Turing’s Thesis

Turing’s thesis (1930):
Any computation carried out by mechanical means can be performed by a Turing Machine
An algorithm for a problem is a Turing Machine which solves the problem

Variations of the Turing Machine

Turing machines with:

• Stay-Option
• Semi-Infinite Tape
• Multitape
• Multidimensional
• Nondeterministic

Same Power of two machine classes:
both classes accept the same set of languages
each new class has the same power with Standard Turing Machine(accept Turing-Recognizable Languages)

Turing Machines with Stay-Option

The head can stay in the same position
L,R,S: possible head moves

• Stay-Option Machines simulate Standard Turing machines
  because any standard Turing machine is also a Stay-Option machine
• Standard Turing machines simulate Stay-Option machines
  because for any transition $q_1\rightarrow q_2[a\rightarrow b,S]$ we can replace it with $q_1\rightarrow q_?[a\rightarrow b,L]$ and $q_?\rightarrow q_2[x\rightarrow x,R]$ for every possible tape symbol $x$

Semi-Infinite Tape

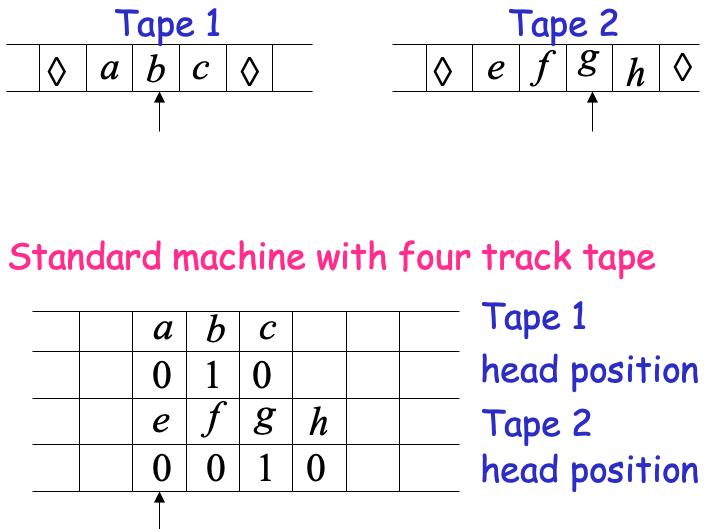
Multiple Track Tape
It is a standard Turing machine, but each tape alphabet symbol describes a pair of actual useful symbols $q_1\rightarrow q_2[(b,a)\rightarrow (c,d),L]$

The head extends infinitely only to the right and Initial position is the leftmost cell. When the head moves left from the border, it returns back to leftmost position

• Standard Turing machines simulate Semi-Infinite machines
  We can insert special symbol # at left of input string and add a self-loop to every state (except states with no outgoing transitions) $q_1\rightarrow q_1[\#\rightarrow \#,R]$
• Semi-Infinite tape machines simulate Standard Turing machines
  choose a reference point and generate a Semi-Infinite tape machine with two tracks(right part and left part)

Multi-tape Turing Machines

$q_1\rightarrow q_2[(b,f)\rightarrow (g,d),L,R]$

• Multi-tape machines simulate Standard Turing machines
  Just use one tape
• Standard Turing machines simulate Multi-tape machines
  Uses a multi-track tape to simulate the multiple tapes. A tape of the Multi-tape machine corresponds to a pair of tracks

Note that same power doesn’t imply same speed
$L=\{a^nb^n\}$, Standard Turing machine needs $O(n^2)$ time but 2-tape machine needs $O(n)$ time(copy $b^n$ to tape 2 and compare tape 1 and tape 2)

Multidimensional Turing Machines

MOVES: L,R,U,D

• Multidimensional machines simulate Standard Turing machines
  Just use one dimension
• Standard Turing machines simulate Multidimensional machines
  Use a two track tape; Store symbols in track 1; Store coordinates in track 2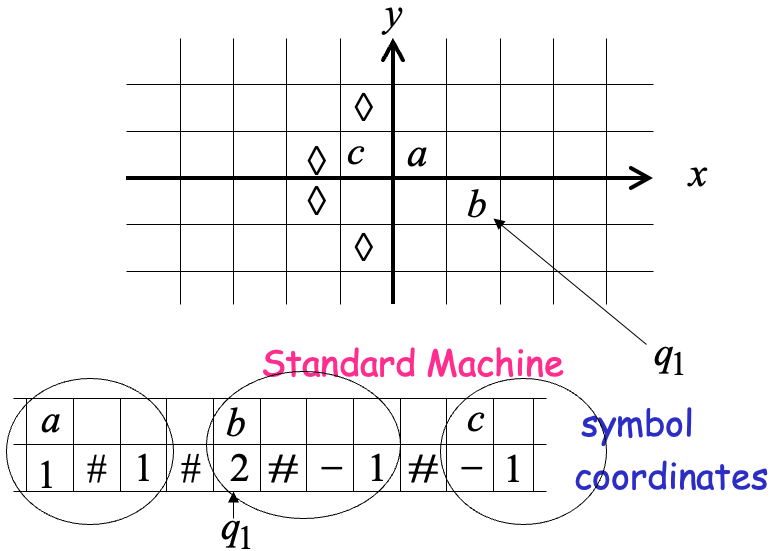

Nondeterministic Turing Machines

• Nondeterministic machines simulate Standard Turing machines
  every deterministic machine is also nondeterministic
• Standard (deterministic) Turing machines simulate Nondeterministic machines
  Uses a 2-dimensional tape(equivalent to standard Turing machine with one tape)

LN19 Universal Turing Machine

A Universal Turing Machine

Tape 1 contents of Universal Turing Machine: binary encoding of the simulated machine $M$ which is description of $M1$ (different numbers of '1's means different symbols while '0's means separators)

A Turing Machine is described with a binary string of 0’s and 1’s
Therefore, the set of Turing machines forms a language: each string of this language is the binary encoding of a Turing Machine

Tape 2 contents of Universal Turing Machine: Tapes Contents of $M$
Tape 3 contents of Universal Turing Machine: State of $M$

Countable Sets

There is a one to one correspondence (injection) of elements of the set to Positive integers (1,2,3,…)
e.g. The set of rational numbers is countable

Let $S$ be a set of strings (Language)
An enumerator for $S$ is a Turing Machine that generates (prints on tape) all the strings of $S$ one by one and each string is generated in finite time

Theorem: The set of all Turing Machines is countable
Proof: Any Turing Machine can be encoded with a binary string of 0’s and 1’s.
Find an enumeration procedure for the set of Turing Machine strings
Enumerator: Repeat:

1. Generate the next binary string of 0’s and 1’s in proper order
2. Check if the string describes a Turing Machine
   if YES: print string on output tape
   if NO: ignore string

Simpler Proof:
Each Turing machine binary string is mapped to the number representing its value

Uncountable Sets

If $S$ is an infinite countable set, then the powerset $2^S$ of $S$ is uncountable.

Since Languages accepted by Turing machines $X$ is countable but All possible languages $2^S$ is uncountable. There is a language not accepted by any Turing Machine.

LN20 Decidable

Decidable Languages

Turing-Acceptable=Turing-Recognizable=Recursively-enumerable

A language $L$ is decidable if there is a Turing machine (decider) $M$ which accepts $L$ and halts on every input string (Also known as recursive languages).

For any input string $w$
If $w\in L$, $M$ halts in an accept state; else $M$ halts in a non-accept state.

Note that Every decidable language is Turing-Acceptable

We can convert any Turing machine to have single accept and reject states
Decider: For each input string, the computation halts in the accept or reject state
Turing Machine for $L$: It is possible that for some input string the machine enters an infinite loop

A computational problem is decidable if the corresponding language is decidable. We also say that the problem is solvable.

Problem: Is number $x$ prime?
Corresponding language: $\text{PRIMES}=\{1,2,3,5,7,\cdots\}$
Decider for $\text{PRIMES}$: On input $x$, divide $x$ with all possible numbers between $2$ and $\sqrt{x}$. If any of them divides $x$ Then reject else accept.

Problem: Does DFA $M$ accpet the empty language $L(M)=\varnothing$?
Corresponding Language: $\text{EMPTY}_{\text{DFA}}=\{\langle M\rangle:M \text{ is a DFA that accpets empty language }\varnothing\}$
Decider for $\text{EMPTY}_{\text{DFA}}$: On input $\langle M\rangle$, Determine whether there is a path from the initial state to any accepting state

Problem: Does DFA $M$ accpet a finite language?
Corresponding Language: $\text{FINITE}_{\text{DFA}}=\{\langle M\rangle:M \text{ is a DFA that accpets a finite language }\}$
Decider for $\text{FINITE}_{\text{DFA}}$: On input $\langle M\rangle$, Check if there is a walk with a cycle from the initial state to an accepting state

$\text{A}_{\text{DFA}}=\{ \langle M,w\rangle: M\text{ is a DFA that accpets string }w \}$

$\text{EQUAL}_{\text{DFA}}=\{ \langle M_1,M_2\rangle: M_1 \text{ and } M_2 \text{ are DFAs that accept the same languages}\}$
Check if $L(M)=(L_1\cap \overline{L_2}) \cup (\overline{L_1}\cap L_2)=\varnothing$
which is a solvable problem for DFAs: $\text{EMPTY}_{\text{DFA}}$

Theorem: If a language $L$ is decidable, then its complement $L$ is decidable too

Undecidable Languages

An undecidable language has no decider: Any Turing machine that accepts $L$ does not halt on some input string

If $L$ is Turing-acceptable but $\overline{L}$ is not Turing-acceptable, $L$ is undecidable such as $L=\{a^i:a^i \in L(M_i)\}$

LN21 Undecidable

Undecidable Problems

Membership problem
$\text{A}_{\text{TM}}=\{ \langle M,w\rangle: M\text{ is a Turing machine that accpets string }w \}$ is Turing-acceptable but undecidable

Halting Problem
$\text{HALT}_{\text{TM}}=\{ \langle M,w\rangle: M\text{ is a Turing machine that halts on input string }w \}$ is Turing-acceptable but undecidable

LN22 Reductions

Reductions

Computable function $f$: There is a deterministic Turing machine $M$ which for any input string $w$ computes $f(w)$ and writes it on the tape

Problem $x$ is reduced to problem $y$: If we can solve problem $y$ then we can solve problem $x$, which means there is a computable function $f$ such that $w\in A\Leftrightarrow f(w)\in B$

Theorem 1:
If: Language $A$ is reduced to $B$ and language $B$ is decidable
Then: $A$ is decidable